Πλακίδιο «αϊνστάιν»: Αυτή είναι η ανακάλυψη που έχει ενθουσιάσει τον κόσμο των μαθηματικών και της φυσικής (φώτο)

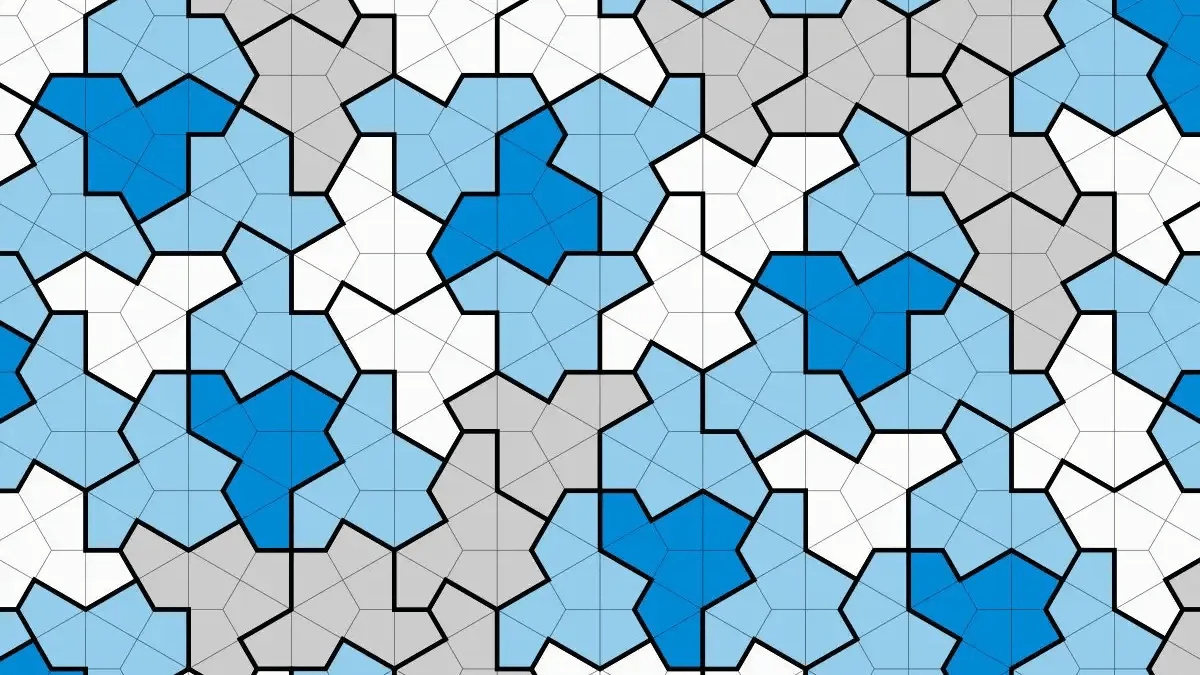
Το πλακίδιο «αϊνστάιν» είναι μία ανακάλυψη ενός μικροσκοπικού σχήματος που φιλοδοξεί να αλλάξει τον κόσμο των μαθηματικών και της φυσικής και τον έχει ενθουσιάσει.

Δεν υπάρχει καμία σχέση με τον διάσημο φυσικό. Εδώ ο όρος «einstein» προέρχεται από τη γερμανική λέξη «ein Stein», που σημαίνει «μια πέτρα», και χρησιμοποιείται για να περιγράψει ένα πολυγωνικό σχήμα που έχει βαφτιστεί ως «καπέλο».

Το «καπέλο» μπορεί να κάνει κάτι που κανένα άλλο γνωστό σχήμα δεν μπορεί να κάνει: συστοιχίζεται με τον εαυτό του με τέτοιο τρόπο ώστε να μπορεί να καλύψει μια άπειρη επιφάνεια χωρίς ποτέ να δημιουργήσει ένα επαναλαμβανόμενο μοτίβο.

Πρόκειται για μια ανακάλυψη που προετοιμαζόταν εδώ και 50 περίπου χρόνια. Το πιο διάσημο μη περιοδικό πλακίδιο –δηλαδή ένα πλακίδιο που δεν επαναλαμβάνεται ποτέ, δημιουργήθηκε από τον Roger Penrose το 1974, αλλά απαιτούσε δύο επιμέρους πλακίδια για να λειτουργήσει. Από τότε, όμως, οι μαθηματικοί αναρωτιούνται: θα μπορούσε να γίνει το ίδιο με τη χρήση ενός μόνο πλακιδίου;

Τώρα, χάρη στον ερασιτέχνη μαθηματικό David Smith, μαζί με μια ομάδα ακαδημαϊκών ερευνητών από το Ηνωμένο Βασίλειο και τις ΗΠΑ, η απάντηση φαίνεται να έχει βρεθεί.

«Όλοι είναι έκπληκτοι και χαρούμενοι», δήλωσε στο Science News η Marjorie Senechal, ομότιμη καθηγήτρια Μαθηματικών και Ιστορίας της Επιστήμης και της Τεχνολογίας στο Smith College, η οποία δεν συμμετείχε στην ανακάλυψη. «Δεν ήταν καν σαφές ότι κάτι τέτοιο θα μπορούσε να υπάρχει».

Προτού ο Smith έρθει σε αυτόν και τους συναδέλφους του με το νέο σχήμα, «θα είχα ζωγραφίσει κάποιο τρελό, τεθλασμένο, δυσάρεστο πράγμα, αν μου ζητούσαν να προτείνω ένα πιθανό πλακίδιο “αϊνστάιν”», δήλωσε στο Science News ο Chaim Goodman-Strauss, καθηγητής Μαθηματικών στο Πανεπιστήμιο του Άρκανσο και συν-συγγραφέας μιας νέας προδημοσίευσης σχετικά με την ανακάλυψη.

Παρόλο που το επιστημονικό άρθρο δεν έχει ακόμα ελεγχθεί επίσημα από την κοινότητα, οι ειδικοί πιστεύουν ότι θα αντέξει στον έλεγχο. Η εύρεση του πλακιδίου και η απόδειξη της μη περιοδικότητάς του απαιτούσε τόσο τη χρήση ισχυρών υπολογιστών όσο και της ανθρώπινης δημιουργικότητας, δήλωσε ο Goodman-Strauss στο New Scientist.

«Ψάχνεις κυριολεκτικά για ένα πράγμα που υπάρχει μία στο εκατομμύριο. Φιλτράρεις τα 999.999 από τα βαρετά, και τότε έχεις μείνει με κάτι που είναι παράξενο και που αξίζει περαιτέρω διερεύνηση».

«Και μετά με το χέρι αρχίζεις να τα εξετάζεις, να προσπαθείς να τα καταλάβεις, και αρχίζεις να συμπεραίνεις τη δομή τους», πρόσθεσε. «Σε αυτό το σημείο ένας υπολογιστής θα ήταν άχρηστος, καθώς θα έπρεπε να συμμετέχει ένας άνθρωπος στην εύρεση μιας κατανοητής απόδειξης».

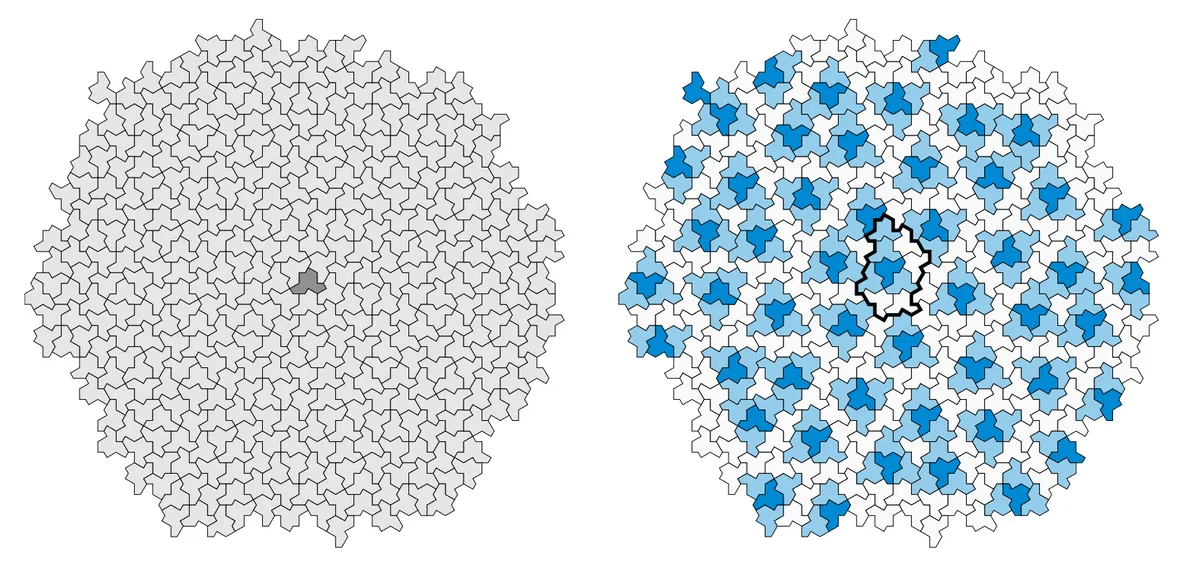
Αυτή η απόδειξη, στην πιο βασική της μορφή, αποτελείται από δύο βήματα. Η πρώτη ένδειξη ότι τα «καπέλα» οργανώνονται σε μεγαλύτερες ομάδες ή «μετα-πλακίδια». Αυτά, με τη σειρά τους, διατάσσονται σε ακόμη μεγαλύτερα «υπερ-πλακίδια», και ούτω καθεξής, μια συμπεριφορά που είναι συνηθισμένη σε μη περιοδικές πλακοστρώσεις, και ήταν μια σημαντική ένδειξη ότι το σχήμα θα μπορούσε να είναι ένα πιθανό πλακίδιο «αϊνστάιν».

Ωστόσο, η απόδειξη της μη περιοδικότητάς του απαιτούσε μια ελαφρώς διαφορετική τεχνική. Για τον σκοπό αυτό η ομάδα επέκτεινε και διαμόρφωσε το «καπέλο» για να δημιουργήσει μια οικογένεια πλακιδίων, όλα με το ίδιο επαναλαμβανόμενο μοτίβο, αλλά σε διάφορα στάδια μεταξύ δύο ακραίων σχημάτων.

Εξετάζοντας την κατάσταση σε αυτά τα άκρα, οι ερευνητές μπόρεσαν να δείξουν ότι το πλακίδιο που δημιουργήθηκε από το καπέλο ήταν όντως μη περιοδικό.

Ενώ το νέο σχήμα μπορεί να ενθουσιάσει τους γεωμέτρες, οι συνέπειες της ανακάλυψης ενός πραγματικού πλακιδίου «αϊνστάιν» εκτείνονται πέρα από το πανεπιστημιακό τμήμα καθαρών μαθηματικών.

Τα μη περιοδικά πλακίδια είναι σημαντικά για την ανάπτυξη των quasi-κρυστάλλων, οι οποίοι με τη σειρά τους έχουν βρει εφαρμογές σε διάφορους τομείς, με πιο εντυπωσιακές τις προσπάθειες δημιουργίας ρομπότ που αλλοιώνουν το σχήμα τους, τύπου Terminator.

Για κάποιους, όμως, οι πιθανές χρήσεις του ομολογουμένως χαριτωμένου νέου σχήματος είναι πιο γήινες και πεζές, ξεκινώντας από το ίδιο το σπίτι:

«Θα δείτε ανθρώπους να τα βάζουν αυτά σε ένα μπάνιο επειδή είναι απλά ωραία», δήλωσε ο Κόλιν Άνταμς, καθηγητής Μαθηματικών στο Κολέγιο Γουίλιαμς, ο οποίος δεν συμμετείχε στην έρευνα. «Εγώ θα τα έβαζα στο μπάνιο μου αν έπρεπε να βάλω πλακάκια αυτή τη στιγμή».