Υπόθεση Ρίμαν: Βραβείο 1 εκατομμυρίου δολαρίων για όποιον λύσει αυτό το μαθηματικό πρόβλημα

Ίδρυμα προσφέρει βραβείο ενός εκατομμυρίου δολαρίων σε όποιον μπορέσει να λύσει ένα διάσημο μαθηματικό πρόβλημα το οποίο προβληματίζει τους μαθηματικούς για περισσότερο από έναν αιώνα.

Η υπόθεση Ρίμαν, που προτάθηκε για πρώτη φορά από τον Γερμανό μαθηματικό Μπέρχαρντ Ρίμαν το 1859, θεωρείται ένα από τα δυσκολότερα και σημαντικότερα άλυτα προβλήματα των καθαρών μαθηματικών – την μελέτης της σκέψης για τα μαθηματικά, αντί της εφαρμογής τους στον πραγματικό κόσμο.

Η υπόθεση βασίζεται στη ζυνάρτηση ζήτα του Ρίμαν, η οποία επίσης αποδίδεται στον Γερμανό μαθηματικό. Η απάντηση στην υπόθεση αυτή είναι ένα απλό «ναι» ή «όχι», αλλά υπάρχουν πολλοί υποθετικοί τρόποι για να φτάσουμε εκεί, οι οποίοι είναι όλοι εξαιρετικά δύσκολοι.

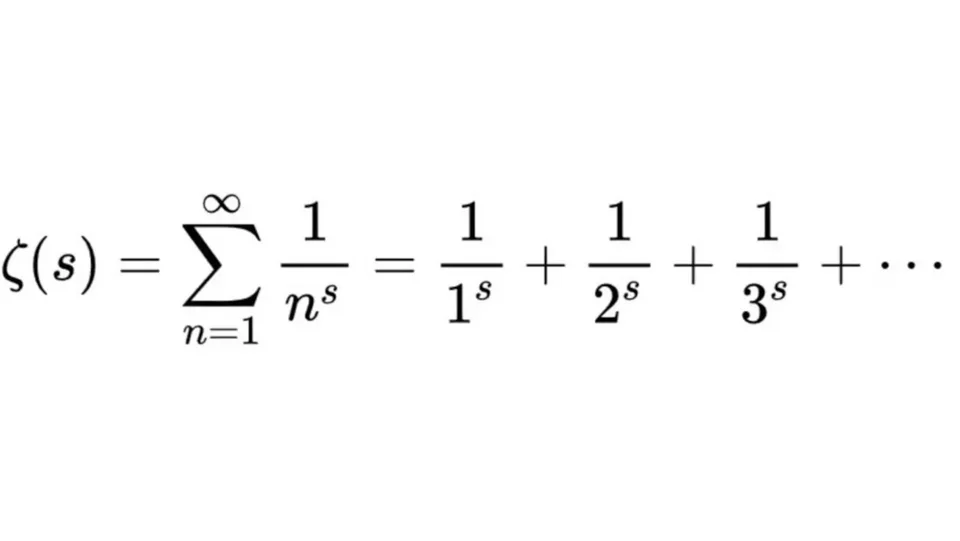
Αν η απάντηση είναι ναι, αυτό θα είχε τεράστιες επιπτώσεις στη θεωρία των αριθμών, την κρυπτογράφηση και τη μελέτη των πρώτων αριθμών, γι’ αυτό και η υπόθεση Ρίμαν αποκαλείται μερικές φορές το «ιερό δισκοπότηρο των μαθηματικών».

Γιατί είναι σημαντική η υπόθεση Ρίμαν;

Αν η υπόθεση Ρίμαν αποδειχθεί αληθής, θα προσφέρει πρωτοποριακές γνώσεις για τη λειτουργία των πρώτων αριθμών.

Ο μαθηματικός, κωμικός και πρώην δάσκαλος Ματ Πάρκερ εξήγησε το 2010 ότι οι ειδικοί έχουν «εμμονή με τους πρώτους αριθμούς, επειδή αποτελούν τη βάση όλων των άλλων αριθμών».

Συγκεκριμένα είπε: «Οι πρώτοι αριθμοί στα μαθηματικά είναι σαν τα άτομα στη χημεία, τα τούβλα στην οικοδομική βιομηχανία και οι γελοίες επιταγές μισθών στο επαγγελματικό ποδόσφαιρο. Τα πάντα χτίζονται από αυτές τις θεμελιώδεις μονάδες και μπορείτε να διερευνήσετε την ακεραιότητα κάποιου πράγματος εξετάζοντας προσεκτικά τις μονάδες από τις οποίες είναι φτιαγμένο. Για να διερευνήσετε πώς συμπεριφέρεται ένας αριθμός, εξετάζετε τους πρώτους παράγοντες του, για παράδειγμα ο 63 είναι 3 x 3 x 7. Οι πρώτοι αριθμοί δεν έχουν παράγοντες: είναι τόσο απλοί όσο μπορούν να γίνουν οι αριθμοί».

Από την άλλη πλευρά, αν η υπόθεση Ρίμαν δεν είναι αληθινή, θα σφετεριστεί πολλά από όσα πιστεύουν οι άνθρωποι για τα μαθηματικά.

Όπως εξηγεί ο νοτιοαφρικανός μαθηματικός Πίτερ Σάρνακ: «Αν (η υπόθεση Ρίμαν) δεν είναι αληθινή, τότε ο κόσμος είναι ένα πολύ διαφορετικό μέρος … Κατά κάποιον τρόπο, θα ήταν πιο ενδιαφέρον αν ήταν ψευδής, αλλά θα ήταν καταστροφή επειδή έχουμε χτίσει τόσα πολλά γύρω από την υπόθεση της αλήθειας της».

Αρκετοί μαθηματικοί έχουν ασχοληθεί με την υπόθεση Ρίμαν κατά τη διάρκεια της 164χρονης ιστορίας της, αλλά καμία από τις προσπάθειές τους δεν έχει γίνει αποδεκτή ως απόδειξη.

Βραβείο 1 εκατομμυρίου δολαρίων για την επίλυση της υπόθεσης Ρίμαν

Το Clay Mathematicians Institute του Cambridge της Μασαχουσέτης προσέφερε 1 εκατομμύριο δολάρια ΗΠΑ σε όποιον μπορέσει να λύσει επαληθεύσιμα το πρόβλημα.

Το 2000, η υπόθεση Ρίμαν χαρακτηρίστηκε ως Πρόβλημα της Χιλιετίας, ένα από τα επτά μαθηματικά προβλήματα που θεωρούνται ζωτικής σημασίας για την αύξηση και τη διάδοση της μαθηματικής γνώσης.

Όποιος λύσει οποιοδήποτε από τα επτά προβλήματα της χιλιετίας δικαιούται την αμοιβή του ενός εκατομμυρίου δολαρίων.